术语科普
- 机器数:在计算机里表示的方法,即正负不再是用
-,+来表示,而是采用0表示正数,1表示负数 - 真数:相对机器数,用
-,+来表示正负的数就叫真数
原码
原码即最原始的二进制表示法,这种方法简单直观。
比如 +11,通常表示为 0000 1011
比如 -11,通常表示为 1000 1011
不知道小伙伴会不会有疑问,那8位可以表示的范围不久小了吗?
答:是的,小了一半。而且 [+0]原 != [-0]原
定义
整数
计算机规定,任何正数的原码都是其本身。而对于负数来说,需要把最高位变为“1”,所以需要 2n - x,由于负负得正,其实是 2n + |x|,其示意图如下所示
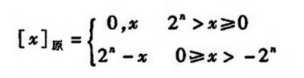
其中x为真值,n为整数的位数
比如:
当x = -1011 时,[x]原 = 24(即1 0000) - (-1011) = 1 1011,即1, 1011
24是指16,16即10000,如果是23,那么就是8,即1000
注意,这里记得用逗号分隔 符号位和数值位
小数
正的小数都是其本身。而对于负数来说,需要把最高位变成“1”,所以需要1 - x,由于负负得正,其实是 1 + |x|,其示意图如下所示
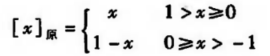
其中x为真值,n为整数的位数
比如:
当x = -0.1011 时,[x]原 = 1 - (-0.1011) = 1.1011
注意,这里记得用点号分隔 符号位和数值位
优点
简单直观
缺点
进行加减运算会带来许多麻烦,比如一个正数和负数相加(注意,这里进行运算时都要采用机器数,不能使用真数)
补码
由于原码在进行四则运算时,总需要判断正负号,所以科学家想到了一种用正数代替负数的方法,即补码
补码的原理类似于 mod(即取余)。比如有一个时钟,现在指向6点,如果想拨到8点钟,我们可以顺时针拨2个小时(可以理解为(6 + 2) mod 12 = 8),也可以逆时针拨10个小时(可以理解为 (12 + (6 - 10)) mod 12 = 8)。这说明了可以用加法代替减法,只要限定最大值,然后不断循环即可。
##定义
整数
计算机规定,正数的补码是其本身;负数的补码要取模 + 真值(为负数)。
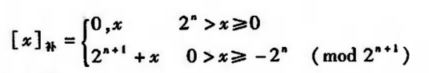
其中x为真值,n为整数的位数
比如:
当 x = -1010 时,[x]补 = 24 + (-1010) = 10000 + (-1010) = 0110
小数
计算机规定,正数的补码是其本身;负数的补码要取2 + 真值(为负数)。
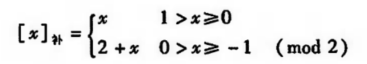
比如:
当 x = -0.1010 时,[x]补 = 2 + (-0.1010) = 10.0000 + (-0.1010) = 1.0110
对于补码来说,由于经常会出现进位的算法,计算时很麻烦,所以这里给出一个简单的算法:
优化
除原码符号位,将其他数值为取反(相当于减),最后加一即可。
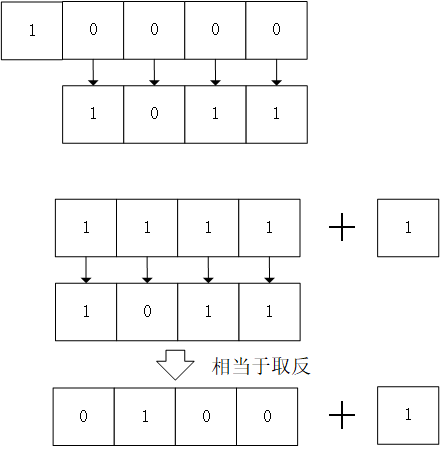
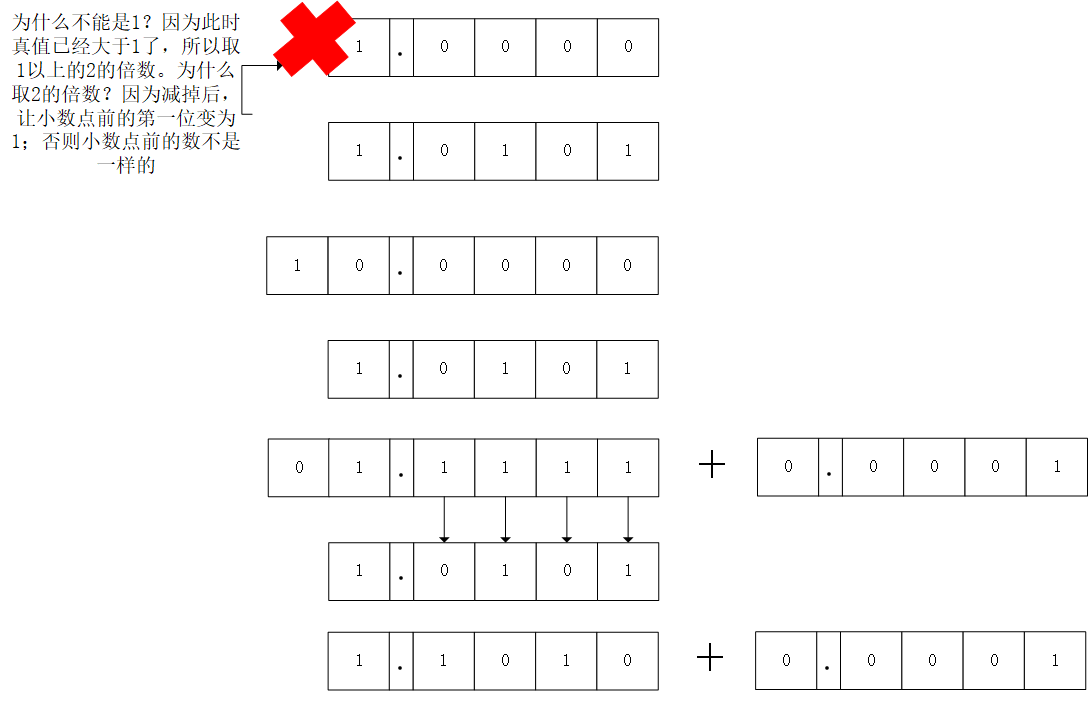
反码
反码其实是补码的一个过渡表示法。将除符号位以外的数值位取反,就可以得到反码(这是我们最直观的做法,但是计算机没那么聪明,需要通过数学公式得到)。
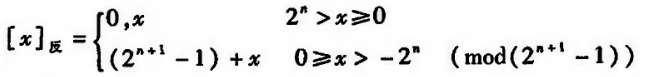
可以很明显发现反码其实就是在补码的基础上减去了一个“1”,就得到了反码。
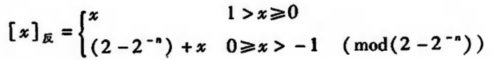
2-n 代表前面有n个0,比如 2 -4,即为0.0001
同理,也是在求补码的基础上减去了一个“1”(这里的“1”对于小数来说是最小的n位)
移码
待我学习一波定点和浮点。